Waves are ubiquitous throughout nature, from water waves to sound waves to light and even matter itself. For this reason, one of my favorite equations is the wave equation,
This is a differential equation, where ∂/∂t notation indicates the derivative operator with respect to the variable t, which I’ll get back to in a moment. In this equation, represents the deformation the wave is making at a given point in space (x,y,z) at a given time t, and c is the speed of the wave. The right hand side is known as the Laplacian of
. Physically, this is a measure of how much
deviates from its average local value. If
is at a minimum,
is positive; it is negative if
is at a maximum.
A derivative is the rate of change of a function, like the deformation . So,
is the rate at which the deformation changes over time. The second derivative, which is in the wave equation, is the rate of change of this rate of change, like how acceleration is the rate of change of velocity, which is itself the rate of change of the position of an object. Thus, the left hand side indicates how the variation in
with respect to time changes in time at a given point in space. These spatial averages and temporal changes feed each other in a constant mutual feedback, resulting in the wave taking on a certain shape. All wave phenomena are governed by this equation (or a slight modification of it). In one dimension, the wave equation simplifies to
which, for pure frequencies/wavelengths has the solutions
where A and B are determined by appropriate boundary conditions (like if a string is fixed at both ends, or free at one end and fixed at the other), is the angular temporal frequency of the wave, and
is the angular spatial frequency of the wave.

(Image: Wikimedia Commons)
This equation can be rewritten in terms of the wavelength (shown above) and period T of the wave,
where is the circle constant. These quantities are related via the speed of the wave,
. These solutions govern things like vibrations of a string, sound made by an air column in a pipe (like that of an organ, trumpet, or didgeridoo), or even waves created by playing with a slinky. They also govern the resonances of certain optical cavities, such as lasers or etalons. Adding up a bunch of waves with pure tones can create waves of almost any imaginable shape, such as this:
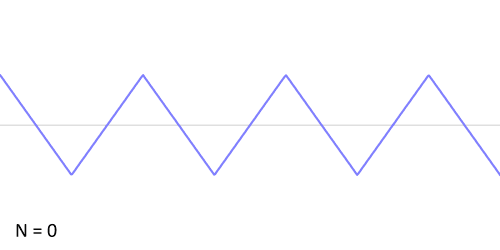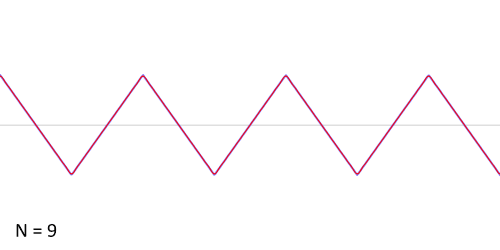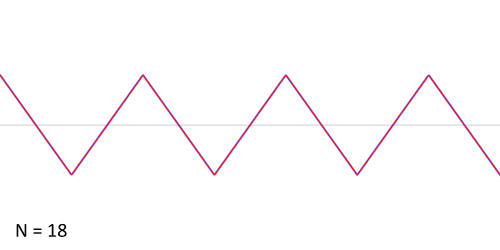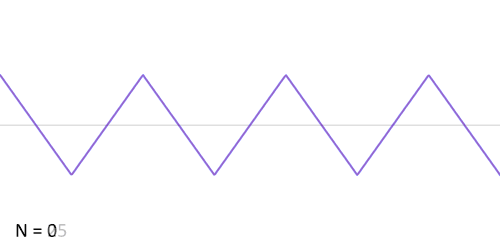
(Image: Wikimedia Commons)
Or this:

(Image: Wikimedia Commons)
Waves do not have to be one dimensional, of course, but I’ll save the two- and three-dimensional cases for another entry.
-A
[…] wave, in general, is any function that obeys the wave equation. To simplify things, though, let’s look at repeating wave […]
LikeLike